Optimal Strategies for Last Man Standing

I have been playing Last Man Standing for about 1 full EPL season now, and ever since I started playing, I have been thinking that there should be a way to play this game optimally. I wanted my first blog post to be about something that I found really interesting, was appropriately nuanced and also relatively novel.

Then, I found this.

This is a beautiful analysis. So beautiful infact that it was actually quite annoying to see. It uses some really neat mathematics. Clearly, I am buoyed by an FA cup weekend off, and hence believe that, whilst exquisite, there are some issues with this modelling that I will try to improve on in this post. As such, we will borrow a lot of the (admittedly standard) formalisation, differing in the strategy that is picked.

The Rules of of Last Man Standing

• The game starts at a given gameweek (GW), with a given sports league(s).
• There are $M$ players each who each put in $x$ amount.
• Each of the $M$ players pick one of the teams that they haven’t currently picked.
• If your team wins, you go through. If your teams draws, or loses, then you go out.
• If all players go out (that is, no one person is left with a winning team after a certain amount of games e.g. all players lose in the last round), then all players have the opportunity to put in $x$ amount again, and all team selection is reset.

A few introductory notes can be gleamed from this.

If you win, your payout is $Mx$. As you pay $x$ to play, your revenue will be $(M-1)x$. If everyone playing picked randomly, then your chance of winning would be $\frac{1}{M}$. Hence, your expected value for this game, if everyone played entirely randomly, is \(\sum_{i=1}^{M-1} \left(-\frac{1}{M} x\right)$ + $\frac{1}{M} \times (M-1)x = 0\). If everyone is playing randomly, then there is no value in this game. But, we don’t want to play randomly! We want to have an optimal strategy for this game. The blog post described a possible optimal strategy, but I believe you can do better.

I have found a few main issues with the previously described strategy:

• It minimises the total chain of probabilities across a full set of games: We only care about the chain of probabilites from the start of the game to the final round of games, no longer!
• It is trying to answer the problem: maximise the length of games that one will win in a row. This is a proxy for the problem that the Last Man Standing game actually rewards: have the longest winning streak out of the $M$ players.
• It assumes that we begin our game of Last Man Standing, give our predictions for all of the games, and then sit back and wait to reap the benefits of our optimal strategy. But that is not how this game is played! After each round, we can see which teams all players have picked (and hence, which teams are available for other players). That is, we gain further information every round we are engaged in.

This is not a static permutation problem, but a constantly updating, multi-stage problem. Let us begin with a formalisation:

Formalisation

• Let there be $n$ teams in the league, labeled $1, 2, \dots, n$.
• Each team $j$ plays a match in each gameweek (GW) $i$. We will ignore the case of double gameweeks.
• Let there be $M$ players in the game, each paying in $x$ amount.
• The state from an individual player’s perspective includes:
  • The current week index $i$.
  • The set of teams this player has already used in previous weeks.
  • The set of teams picked by all other players.
  • The amount of other players still involved.
• The actions an indvidual player may take are the choice of team $j$.
• Let $p_j^{(i)}$ denote the probability that team $j$ wins its match in week $i$.

We may visualise the entire game through the below graphic. Each node through this graph is a team, with winning and losing teams coloured green and red respectively. Each edge between a node is a choice of team $j$ at GW $i+1$ from GW $i$. In this representation, there are $k$ steps before an individual player wins.

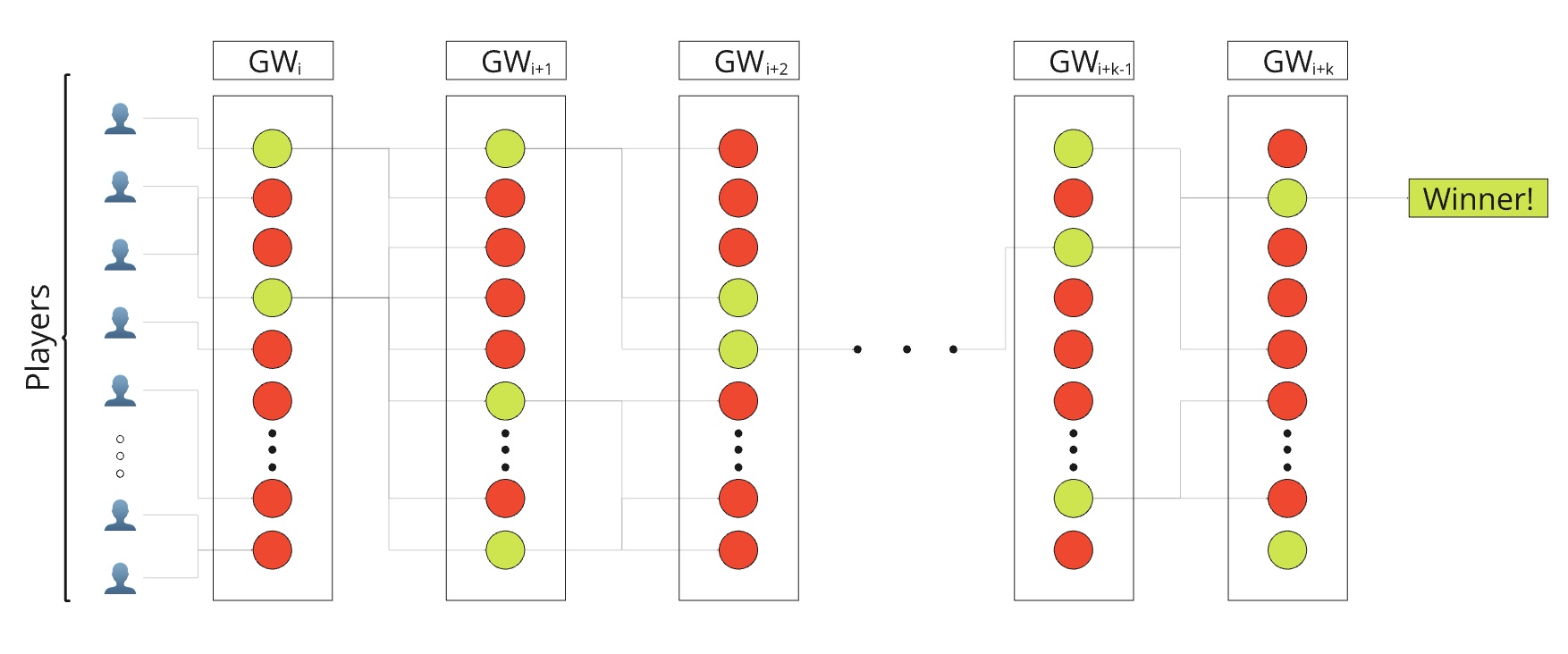
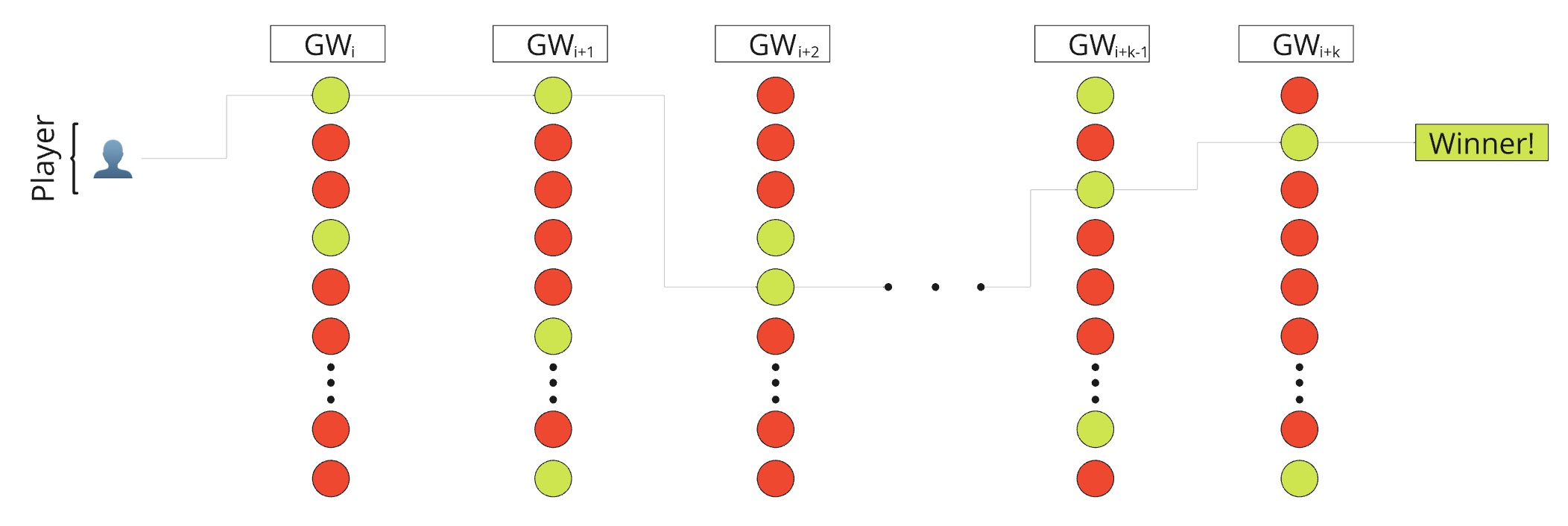
We want to successfully navigate through this graph, where after $k$ choices of team, only we remain. We want out results to look like below:

1. Dynamic Programming / Markov Decision Process (MDP) Formulation

Instead of pre-committing to a full permutation of teams, you can view the problem as a multi-stage decision process. In this formulation:

• State: A state at gameweek $i$ includes:
  • The current gameweek index $i$.
  • The set of teams you have already used.
  • Information about the number of surviving players and the teams that they have already picked.

• Actions: At each stage (gameweek), the action is to choose one of the remaining teams.

• Transition: The system transitions to the next state based on:
  • The match outcome for the team you selected, governed by the probability $p_j^{(i)}$ (and possibly the outcomes of matches for other players).
  • Updates to your available team pool (since you cannot pick a team twice).
• Reward / Objective:
  • Reward of $(M-1)*x$ at the end of the game if you are the sole winner, with a negative payoff of $-x$ if you are not the winner. We may similarly just use a reward of 1 every time our choice of team wins, and a reward of 0 everytime a team we choose does not win. We may have our reward model as the multiple of all rewards until the end of the game.

The objective is to maximize the probability of eventually reaching a terminal state in which you are the only player remaining.

This dynamic programming approach (or MDP formulation) captures the sequential nature of the game and can incorporate the evolving state of the competition. However, the state space may be very large, so you might need to use approximate dynamic programming methods or simulation-based techniques.

Now we have established a theoretical framework, let us begin with our experiments.

(experiments go here (-:))

Another option is:

2. Simulation and Bayesian Learning

Another alternative is to adopt a simulation-based approach:

• Simulate the Competition: Create a simulator that models match outcomes (using the probabilities ($p_j^{(i)}$) and the elimination process for all players.

• Bayesian or Reinforcement Learning: Use simulation to learn which sequences of picks tend to yield the highest probability of being the sole survivor:

  • Bayesian updating of your beliefs about opponents’ strategies.
  • Reinforcement learning techniques (Q-learning) to evaluate the long-term benefits of each action.

This approach will require a hefty amount of nuanced work!